MTH240 Engineering Mathematics I Assignment: Heat Transfer, Chemical Balancing, Circuit Analysis, Signal Processing, and Matrix Theory

MTH240 Engineering Mathematics I Tutor-Marked Assignment

Question 1

Consider the cross section of a long rectangular metallic plate. The edges of this plate are being kept at specific, constant temperatures. engineers want to know: what is the temperature inside the plate? This is important because if parts of the plate get hotter or colder, it could cause stress and damage over time.

We assume that the temperatures on the edges don’t change over time. Eventually, the heat inside the plate will settle into a steady pattern — this is called thermal equilibrium. At that point, the temperature at every point inside the plate stops changing.

Finding the temperature at every point inside the plate exactly is really hard. But we can estimate the temperature at some key points using a neat idea from physics called the MeanValue Property:

• If the plate is in thermal equilibrium and you look at a point inside the plate (not on the edge), then the temperature at that point is the average of the temperatures at the four neighboring points (up, down, left, and right).

Below is a diagram showing a simplified grid representing the rectangular plate. The temperatures along the edges are fixed and shown in degrees Celsius. The interior points of the plate are labeled a, b, c, and d — these are the points where we want to estimate the temperatures.

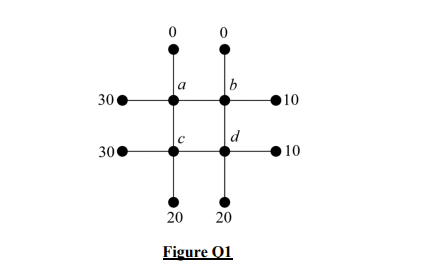
(a) Using the Mean-Value Property, write a system of linear equations to represent the temperatures at the interior points a, b, c, and d. Show all steps.

(5 marks)

(b) Use Gaussian elimination method to determine the temperatures at the interior nodes. Verify your answer.

(10 marks)

(c) Consider the coefficient matrix from your system in part (a).

(i) Compute a basis for the row space and the column space of this matrix.

(2 marks)

(ii) Briefly interpret what the column space represents in the context of temperature distribution on the plate.

(3 marks)

Question 2

Linear algebra techniques can also be applied in Chemistry, particularly in balancing chemical reactions. Consider the following chemical reaction:
𝑆𝑛𝑂2 + 𝐻2 → 𝑆𝑛 + 𝐻2𝑂

This reaction involves tin (𝑆𝑛), oxygen (O), and hydrogen (H), where tin dioxide (𝑆𝑛𝑂2) and hydrogen (𝐻2) react to form tin (𝑆𝑛) and water (𝐻2𝑂). To analyze this, we apply mass balance theory, which states that elements cannot be created or destroyed in a reaction. This means the number of atoms for each element must be the same on both sides.

(a) Set up the system of linear equations to balance this chemical reaction.

(2 marks)

(b) Use Gaussian elimination method to solve the system of linear equations.

(3 marks)

(c) Consider the coefficient matrix from your system in part (a).

(i) Determine a basis for the row space and the column space of the matrix.

(2 marks)

(ii) Explain what the column space represents in the context of balancing chemical equations, and why it’s important.

(3 marks)

Question 3

Use Loop Current Analysis of Electric Circuits to find the currents in the circuit below.

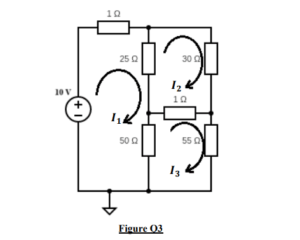
(a) Apply Kirchoff‟s Voltage Law for each loop to set up a system of linear equations.

(5 marks)

(b) Solve the system of equations using the Gaussian Elimination method to find 𝐼1, 𝐼2, and 𝐼3.

(10 marks)

(c) Consider the coefficient matrix from the system in part (a):

(i) Find a basis for the row space and the column space of the matrix.

(ii) Explain what the column space represents in the context of circuit analysis,
particularly in relation to current conservation and solvability.

(5 marks)

Question 4

In biomedical engineering, electrocardiogram (ECG) signals are used to monitor the electrical activity of the heart. However, these signals often become contaminated with noise from muscle movement, power line interference, or electronic components.

To remove noise, engineers project the ECG signal onto a subspace that contains only the valid ECG patterns. This subspace can be defined using a few known clean signal vectors. To perform the projection efficiently, an orthonormal basis for this subspace must first be constructed.

Suppose you are given the following three clean ECG pattern vectors, each representing a small segment of sampled ECG data over time:

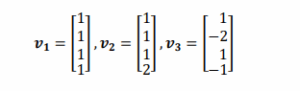
(a) Use the Gram-Schmidt process to compute an orthonormal basis for the subspace 𝑼 of ℝ𝟒 spanned by {𝒗𝟏, 𝒗𝟐, 𝒗𝟑}. Show all steps: projection, subtraction, and normalization. Label your final orthonormal basis vectors as 𝒆𝟏, 𝒆𝟐, 𝒆𝟑

(10 marks)

(b) Explain why the vectors {𝒗𝟏, 𝒗𝟐, 𝒗𝟑} are linearly independent, and what would happen in the Gram-Schmidt process if they were not. Provide a check using determinants or rank and describe how you would proceed if linear dependence occurred.

(5 marks)

(c) Using an orthonormal basis makes filtering fast and accurate because each coefficient is simply a dot product. There’s no overlap between directions, which ensures clean separation of signal components. This is crucial in ECG processing to isolate meaningful heart signals from interference and noise. A noisy ECG signal segment is recorded as:

𝒔𝒏𝒐𝒊𝒔𝒆 =
[2
1
2
1]

Project 𝒔𝒏𝒐𝒊𝒔𝒆 onto the subspace spanned by your orthonormal basis {𝒖𝟏, 𝒖𝟐, 𝒖𝟑}, and compute the filtered signal 𝒔𝒇𝒊𝒍𝒕𝒆𝒓𝒆𝒅 using:

𝒔𝒇𝒊𝒍𝒕𝒆𝒓𝒆𝒅 = (𝒔𝒏𝒐𝒊𝒔𝒆𝑻∙ 𝒆𝟏)𝒆𝟏 + (𝒔𝒏𝒐𝒊𝒔𝒆𝑻∙ 𝒆𝟐)𝒆𝟐 + (𝒔𝒏𝒐𝒊𝒔𝒆𝑻∙ 𝒆𝟑)𝒆

(5 marks)

Question 5

In real-life engineering problems different parts of a system often affect each other. For example:

• In a chemical plant, the concentration of a substance in one tank may depend on what’s happening in nearby tanks.
• In a mechanical system, the movement of one part might affect another.
  When this happens, we say the system is coupled, and we can describe it using a set of equations like:

𝑑𝒙/𝑑𝑡 = 𝐴

Here:

• 𝒙 = [𝑥1(𝑡)𝑥2(𝑡)…𝑥𝑛(𝑡)] representing the system variables
• 𝐴 is an n×n constant system matrix that describes how each variable affects the others

(a) This equation is “coupled” because, in general, each component 𝑑𝑥𝑖
𝑑𝑡 depends on a linear combination of all 𝑥𝑖 variables (i.e., the off-diagonal elements of A are non-zero).

Solving this set of coupled equations directly is hard, because all the variables are mixed together.

(a) Show that by transforming 𝒙 = 𝑃𝒚 where P is a matrix such that the columns of 𝑃 are the eigenvectors of A , and 𝒚 = [ 𝑦1 (𝑡) 𝑦2 (𝑡) … 𝑦(𝑡) ] is a new variable, we can convert the original coupled system into a decoupled system of the form:

𝑑𝒚/𝑑𝑡 = 𝐷𝒚

Clearly explain why this new system is considered “decoupled” compared to the original one.

(b) Consider a simplified chemical reaction network within three interconnected reactors 𝑅1, 𝑅2, 𝑅3. Let 𝑥1(𝑡), 𝑥2(𝑡), and 𝑥3(𝑡) represent the concentrations of a specific reactant in each reactor at time 𝑡. The rates of change of these concentrations are governed by the following linear differential equations, which model the reaction kinetics and mass transfer between reactors:

𝑑𝑥1/𝑑𝑡 = 𝑥1 + 2𝑥2
𝑑𝑥2/𝑑𝑡 = 2𝑥1 + 𝑥2
𝑑𝑥3/𝑑𝑡 = 3𝑥3

(i) Identify and write down the 3×3 system matrix A from the given set of differential equations.

(1 marks)

(ii) Evaluate all the eigenvalues of A.

(3 marks)

(iii) For each eigenvalue found, determine its corresponding eigenvector. If an
eigenvalue is repeated, ensure you find a set of linearly independent eigenvectors corresponding to its multiplicity.

(9 marks)

(iv) Diagonalise the matrix A and hence find the undecoupled system
𝑑𝒚/𝑑𝑡 = 𝐷𝒚.

(2 marks)

Question 6

𝐴 =
[5 4 2
0 5 1
0 0 5]

(a) Show that matrix A is not diagonalizable.

(3 marks)

(b) Find the Jordan normal form of A.

(3 marks)

(c) Find the generalised eigenvectors.

(4 marks)

 

The post MTH240 Engineering Mathematics I Assignment: Heat Transfer, Chemical Balancing, Circuit Analysis, Signal Processing, and Matrix Theory appeared first on Singapore Assignment Help.